Как строить сечения по трем точкам. Построение сечений и разрезов на чертежах

Аксиомы планиметрии:

В различных учебниках свойства прямых и плоскостей могут быть представлены по-разному, в виде аксиомы, следствия из нее, теоремы, леммы и т.д. Рассмотрим учебник Погорелова А.В.

Прямая разбивает плоскость на две полуплоскости.

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Аксиомы стереометрии:

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие этой плоскости, и точки не принадлежащие ей.

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

Из трех точек на прямой одна и только одна лежит между двумя другими.

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 0 . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.

На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Сечение

В пространстве две фигуры, для нашего случая плоскость и многогранник могут иметь следующее взаимное расположение: не пересекаются, пересекаются в точке, пересекаются по прямой и плоскость пересекает многогранник по его внутренности (рис.1), и при этом образуют следующие фигуры:

а) пустая фигура (не пересекаются)

б) точка

в) отрезок

г) многоугольник

Если в пересечении многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника с плоскостью .

рис.1

Определение. Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела с плоскостью.

Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.

Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом, пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок.

Если плоскости пересекаются по прямой, то прямую называют следом одной из этих плоскостей на другой.

В общем случае секущая плоскость многогранника пересекает плоскость каждой его грани (а также любую другую секущую плоскость этого многогранника). Она пересекает и каждую из прямых, на которых лежат ребра многогранника.

Прямую, по которой секущая плоскость пересекает плоскость какой-либо грани многогранника, называют следом секущей плоскости на плоскости этой грани, а точку, в которой секущая плоскость пересекает прямую, содержащую какое – либо ребро многогранника, называют следом секущей плоскости на этой прямой. Эта точка является и следом прямой на секущей плоскости. Если секущая плоскость пересекает непосредственно грань многогранника, то можно говорить о следе секущей плоскости на грани, и, аналогично, о следе секущей плоскости на ребре многогранника, то есть о следе ребра на секущей плоскости.

Так как прямая однозначно определяется двумя точками, то для нахождения следа секущей плоскости на любой другой плоскости и, в частности, на плоскости любой грани многогранника, достаточно построить две общие точки плоскостей

Для построения следа секущей плоскости, а также для построения сечения многогранника этой плоскостью, должен быть задан не только многогранник, но и секущая плоскость. А построение плоскости сечения проходит в зависимости от задания этой плоскости. Основными способами задания плоскости, и в частности секущей плоскости, являются следующие:

тремя точками не лежащих на одной прямой;

прямой и не лежащей на ней точкой;

двумя параллельными прямыми;

двумя пересекающимися прямыми;

точкой и двумя скрещивающимися прямыми;

Возможны и другие способы задания секущей плоскости.

Поэтому все способы построения сечений многогранников можно разделить на методы.

Методы построения сечений многогранников

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Существует три основных метода построения сечений многогранников:

Аксиоматический метод:

Метод следов.

Комбинированный метод.

Координатный метод.

Заметим , что метод следов и метод вспомогательных сечений являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

построение сечения, проходящего через заданную прямую параллельно, другой заданной прямой;

построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;

построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;

построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

Основными действиями, составляющие методы построения сечений, являются нахождение точки пересечения прямой с плоскостью, построения линии пересечения двух плоскостей, построение прямой параллельной плоскости, перпендикулярной плоскости. Для построения прямой пересечения двух плоскостей обычно находят две ее точки и проводят через них прямую. Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную. Тогда искомая точка получается в пересечении найденной прямой с данной.

Рассмотрим отдельно перечисленные нами методы построения сечений многогранников:

Метод следов.

Метод следов основывается (операеться) на аксиомах стереометрии, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют основным следом секущей плоскости . Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.

Отметим, что при построении основного следа секущей плоскости используется следующее утверждение.

Если точки принадлежат секущей плоскости и не лежат на одной прямой, а их проекция (центральными или параллельными) на плоскость, выбранную в качестве основной, являются соответственно точки то точки пересечения соответственных прямых, то есть точки и лежат на одной прямой (рис.1, а, б).

рис.1.а рис.1.б

Эта прямая является основным следом секущей плоскости. Так как точки лежат на основном следе, то для его построения достаточно найти две точки из этих трех.

Метод вспомогательных сечений.

Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее, в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Комбинированный метод

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Координатный метод построения сечений.

Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.

Заметим , что это способ построения сечения многогранника приемлем для компьютера, так как он связан с большим объемом вычислений и поэтому этот метод целесообразно реализовать с помощью ЭВМ.

Наша основная задача будет состоять в построении сечения многогранника с плоскостью, т.е. в построении пересечения этих двух множеств.

Построение сечений многогранников

Прежде всего заметим, что сечение выпуклого многогранника есть выпуклый плоский многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многогранника, а стороны с его гранями.

Примеры построения сечений:

Способы задания сечения весьма разнообразны. Наиболее распространенным из них является способ задания секущей плоскости тремя точками, не лежащими на одной прямой.

Пример 1. Для параллелепипеда ABCDA 1 B 1 C 1 D 1 . Построить сечение проходящее через точки M, N, L.

Решение:

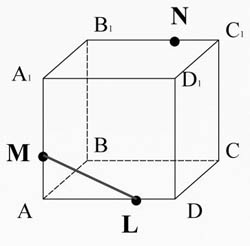
Соединим точки M и L, лежащие в плоскости AA 1 D 1 D.

Пересечем прямую ML (принадлежащую сечению) с ребром A 1 D 1 1 D 1 D. Получим точку X 1 .

Точка X1 лежит на ребре A 1 D 1 , а значит и плоскости A 1 B 1 C 1 D 1 , соединим ее сточкой N, лежащей в этой же плоскости.

X 1 N пересекается с ребром A 1 B 1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA 1 B 1 B.

Найдем прямую пересечения плоскости сечения с плоскостью DD 1 C 1 C:

Пересечем прямую ML (принадлежащую сечению) с ребром DD 1 , они лежат в одной плоскости AA 1 D 1 D, получим точку X 2 .

Пересечем прямую KN (принадлежащую сечению) с ребром D 1 C 1 , они лежат в одной плоскости A 1 B 1 C 1 D 1 , получим точку X3;

Точки X2 и X3 лежат в плоскости DD 1 C 1 C. Проведем прямую X 2 X 3 , которая пересечет ребро C 1 C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника, что и мы сделали. MKNTPL - искомое сечение.

Заметим. Эту же самую задачу на построение сечения, можно решить воспользуевавшийся свойством параллельных плоскостей.

Из выше сказанного можно составить алгоритм (правило) решения задач, данного типа.

Правила построения сечений многогранников:

Пример 2. D L , M

Решим аксиоматическим методом:

Проведем вспомогательную плоскость DKM , которая пересекает ребра АВ и ВС в точках Е и F (ход решение на рис 2.). Построим «след» КМ плоскости сечения на этой вспомогательной плоскости, найдем точку пересечения КМ и Е F – точку Р. Точка Р, как и L , лежит в плоскости АВС, и можно провести прямую, по которой плоскость сечения пересекает плоскость АВС(«след» сечения в плоскости АВС).

Пример 3. На ребрах AB и AD пирамиды MABCD зададим соответственно точки P и Q - середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Решение проведем комбинированным методом:

1). Ясно, что основным следом плоскости PQR является прямая PQ.

2). Найдем точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.

3). Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.

4). Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ - средняя линия треугольника ABD, то PQ параллена BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.

5). Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD"RB" - искомое сечение

Рассмотрим сечения призмы для простоты, то есть удобства логических размышлений рассмотрим сечения куба (рис.3.а):

Рис. 3.а

Сечения призмы плоскостями, параллельными боковым ребрам, является параллелограммами. В частности, параллелограммами являются диагональные сечения (рис. 4).

Опр. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Многоугольник, получающийся при диагональном сечении призмы, является параллелограммом. Вопрос о числе диагональных сечений n -угольной призмы труднее, чем вопрос о числе диагоналей. Сечений будет столько же сколько диагоналей у основания. Мы знаем, что у выпуклой призмы в основаниях – выпуклые многоугольники, а у выпуклого n -угольника диагоналей. И так можно говорить, что диагональных сечений вдвое меньше, чем диагоналей.

Заметим: При построении сечений параллелепипеда на рисунке следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким – то отрезкам, то эти отрезки параллельны «по свойству параллелепипеда т.е. противоположные грани параллелепипеда параллельны и равны.»

Дадим ответы на часто возникающие вопросы:

Какие многоугольники получаются в сечении куба плоскостью?

«треугольник, четырехугольник, пятиугольник, шестиугольник ».

Может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник?

«не могут».

3)Возникает вопрос чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника .

Пример 3. Построить сечение призмы A 1 B 1 C 1 D 1 ABCD плоскостью, проходящей через три точки M, N, K.

Рассмотрим случай расположения точек M, N, K на поверхности призмы (рис. 5).

Рассмотрим случай: В данном случае очевидно, что M1 = B1.

Построение:

Пример 4. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.6)).

Решение:

Рис. 6

Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х.

Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.

Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.

Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два не соседних боковых ребра пирамиды.

Пример 4. Построить сечение пирамиды АВС D плоскостью, проходящей через точки К, L , M .

Решение:

Этот же пример решим по другому .

Допустим что по точкам К, L , и М построено сечение KLNM (рис. 7). Обозначим через F точку пересечения диагоналей четырехугольника KLNM . Проведем прямую DF и обозначим через F 1 ее точку пересечения с гранью АВС. Точка F 1 совпадает с точкой пересечения прямых АМ и СК (F 1 одновременно принадлежит плоскостям АМ D и D СК). Точку F 1 легко построить. Далее строим точку F как точку пересечения DF 1 и LM . Далее находим точку N .

Рассмотренный прием называют методом внутреннего проектирования . (Для нашего случая речь идет о центральном проектировании. Четырехугольник K МСА есть проекция четырехугольника KMNL из точки D . При этом точка пересечения диагоналей KMNL – точка F – переходит в точку пересечения диагоналей четырехугольника K МСА – точку F 1 .

Площадь сечения многогранника.

Задача на вычисление площади сечения многогранника обычно решается в несколько этапов. Если в задаче говориться, что сечение построено (или что секущая плоскость проведена и т.п.), то на первом этапе решения выясняют вид фигуры полученной в сечении.

Это необходимо сделать, чтобы выбрать соответствующую формулу для вычисления площади сечения. После того как вид фигуры, полученной в сечении, выяснен и выбрана формула для подсчета площади этой фигуры, переходят непосредственно к вычислительной работе.

В некоторых случаях может оказаться проще, если, не выясняя вида фигуры, полученной в сечении, перейти сразу к вычислениям ее площади по формуле, которая следует из теоремы.

Теорема о площади ортогональной проекции многоугольника: площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: .

Справедлива формула для вычисления площади сечения: где это площадь ортогональной проекции фигуры, полученной в сечении, аэто угол между секущей плоскостью и плоскостью, на которую фигура спроектирована. При таком ходе решения необходимо построить ортогональную проекцию фигуры, полученной в сечении, и подсчитать

Если в условии задачи говориться, что сечение требуется построить и найти площадь полученного сечения, то на первом этапе следует обосновано выполнить построение заданного сечения, и затем, естественно, определить вид фигуры, полученной в сечении, и т.д.

Отметим следующий факт: так как строятся сечения выпуклых многогранников, то многоугольник сечения будет тоже выпуклым, поэтому его площадь можно найти разбиением на треугольники, то есть площадь сечения равна сумме площадей треугольников из которых оно составлено.

Задача 1.

– правильная треугольная пирамида со стороной основания равной и высотой равной Постройте сечение пирамиды плоскостью, проходящей через точки, где – середина стороны, и найдите его площадь (рис.8).

Решение.

Сечением пирамиды является треугольник. Найдем его площадь.

Так как основание пирамиды – равносторонний треугольник и точка – середина стороны, то является высотой и тогда, .

Площадь треугольника можно найти:

Задача 2.

Боковое ребро правильной призмы равно стороне основания. Построить сечения призмы плоскостями, проходящими через точку A , перпендикулярно прямой Если найти площадь полученного сечения призмы.

Решение.

Построим заданное сечение. Сделаем это из чисто геометрических соображений, например, следующим образом.

В плоскости проходящей через заданную прямую и заданную точку проведем через эту точку прямую, перпендикулярную прямой (рис. 9). Воспользуемся с этой целью тем, что в треугольнике то есть его медиана является и высотой этого треугольника. Таким образом, прямая.

Через точку проведем еще одну прямую, перпендикулярную прямой. Проведем ее, например, в плоскости, проходящей через прямую. Ясно, что этой прямой является прямая

Итак, построены две пересекающиеся прямые, перпендикулярные прямой. Этими прямимы определяется плоскость, проходящая через точку перпендикулярно прямой то есть задана секущая плоскость.

Построим сечение призмы этой плоскостью. Заметим, что так как, то прямая параллельна плоскости. Тогда плоскость, проходящая через прямую, пересекает плоскость по прямой, параллельной прямой, то есть и прямой. Проведем через точку прямую и полученную точку соединим точкой.

Четырехугольник заданное сечение. Определим его площадь.

Понятно что четырехугольник является прямоугольником, то есть его площадь

рис. 9

Сегодня еще раз разберем, как построить сечение тетраэдра плоскостью .
Рассмотрим самый простой случай (обязательный уровень), когда 2 точки плоскости сечения принадлежат одной грани, а третья точка - другой грани.

Напомним алгоритм построения сечений такого вида (случай: 2 точки принадлежат одной грани).

1. Ищем грань, которая содержит 2 точки плоскости сечения. Проводим прямую через две точки, лежащие в одной грани. Находим точки ее пересечения с ребрами тетраэдра. Часть прямой, оказавшаяся в грани, есть сторона сечения.

2. Если многоугольник можно замкнуть - сечение построено. Если нельзя замкнуть, то находим точку пересечения построенной прямой и плоскости, содержащей третью точку.

1. Видим, что точки E и F лежат в одной грани (BCD), проведем прямую EF в плоскости (BCD).
2. Найдем точку пересечения прямой EF c ребром тетраэдра BD, это точка Н.
3. Теперь следует найти точку пересечения прямой EF и плоскости, содержащей третью точку G, т.е. плоскости (ADC).
Прямая CD лежит в плоскостях (ADC) и (BDC), значит она пересекается с прямой EF, и точка К является точкой пересечения прямой EF и плоскости (ADC).
4. Далее находим еще две точки, лежащие в одной плоскости. Это точки G и K, обе лежат в плоскости левой боковой грани. Проводим прямую GK, отмечаем точки, в которых эта прямая пересекает ребра тетраэдра. Это точки M и L.
4. Осталось "замкнуть" сечение, т.е.соединить точки, лежащие в одной грани. Это точки M и H, и также L и F. Оба этих отрезка - невидимы, проводим их пунктиром.

В сечении получился четырехугольник MHFL. Все его вершины лежат на ребрах тетраэдра. Выделим получившееся сечение.

Теперь сформулируем "свойства" правильно построенного сечения:

1. Все вершины многоугольника, которое является сечением, лежат на ребрах тетраэдра (параллелепипеда, многоугольника).

2. Все стороны сечения лежат в гранях многогранника.
3. В каждой грани многоранника может находиться не более одной (одна или ни одной!) стороны сечения

Цель работы:
Развитие пространственных представлений.
Задачи:
1. Познакомить с правилами построения сечений.
2. Выработать навыки построения сечений
тетраэдра и параллелепипеда при различных
случаях задания секущей плоскости.
3. Сформировать умение применять правила
построения сечений при решении задач по
темам «Многогранники».

Для решения многих
геометрических
задач необходимо
строить сечения
многогранников
различными
плоскостями.

Понятие секущей плоскости

Секущей
плоскостью
параллелепипеда
(тетраэдра)
называется любая
плоскость, по обе
стороны от
которой имеются
точки данного
параллелепипеда
(тетраэдра).

Понятие сечения многогранника

Секущая плоскость
пересекает грани
тетраэдра
(параллелепипеда) по
отрезкам.
Многоугольник, сторонами
которого являются данные
отрезки, называется
сечением тетраэдра
(параллелепипеда).

Работа по рисункам

Сколько плоскостей можно провести
через выделенные элементы?
Какие аксиомы и теоремы вы применяли?

Для построения сечения
нужно построить точки
пересечения секущей
плоскости с ребрами и
соединить их отрезками.

Правила построения сечений

1. Соединять можно только две
точки, лежащие в плоскости одной
грани.
2. Секущая плоскость пересекает
параллельные грани по
параллельным отрезкам.

Правила построения сечений

3. Если в плоскости грани отмечена
только одна точка, принадлежащая
плоскости сечения, то надо
построить дополнительную точку.
Для этого необходимо найти точки
пересечения уже построенных
прямых с другими прямыми,
лежащими в тех же гранях.

10. Построение сечений тетраэдра

11.

Тетраэдр имеет 4 грани
В сечениях могут получиться
Треугольники
Четырехугольники

12.

Построить сечение тетраэдра
DABC плоскостью, проходящей
через точки M,N,K
1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
D
M
AA
N
K
BB
CC
2. Проведем прямую через
точки К и N, т.к. они
лежат в одной грани
(СDB).
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK –
искомое сечение.

13. проходящей через точку М параллельно АВС.

D
1. Проведем через точку М
прямую параллельную
ребру AB
2.
М
Р
А
К
С
В
Проведем через точку М
прямую параллельную
ребру AC
3. Проведем прямую через
точки K и P, т.к. они лежат в
одной грани (DBC)
4. Треугольник MPK –
искомое сечение.

14.

Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
D
1. Проводим КF.
2. Проводим FE.
3. Продолжим
EF, продолжим AC.
F
4. EF AC =М
5. Проводим
MK.
E
M
AB=L
6.
MK
C
A
7. Проводим EL
L
EFKL – искомое сечение
K
B

15.

Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K
СКакие
какойпрямые
точкой,
лежащей в
можно
Соедините
получившиеся
Какие
точки
можно
сразу
той
же
грани
можно
продолжить,
чтобы
получить
точки,
лежащие
в
одной
соединить?
соединить
полученную
дополнительную
точку?
грани,
назовите
сечение.
дополнительную точку?
D
АС
ЕLFK
FСЕК
иточкой
K,и Е
и FК
F
L
C
M
A
E
K
B

16.

Построить сечение
тетраэдра плоскостью,
проходящей через точки
E, F, K.
D
F
L
C
A
E
K
B
О

17.

Вывод: независимо от способа
построения сечения одинаковые

18. Построение сечений параллелепипеда

19.

Тетраэдр имеет 6 граней
Треугольники
Пятиугольники
В его сечениях могут получиться
Четырехугольники
Шестиугольники

20. Построить сечение параллелепипеда плоскостью проходящей через точку Х параллельно плоскости (ОСВ)

В1
А1
Y
Х
D1
S
В
А
D
Z
1. Проведем через
С1
точку X прямую
параллельную ребру
D1C1
2. Через точку X
прямую
параллельную ребру
D1D
3. Через точку Z прямую
параллельную ребру
С
DC
4. Проведем прямую через
точки S и Y, т.к. они лежат в
одной грани (BB1C1)
XYSZ – искомое сечение

21.

Построить сечение параллелепипеда
плоскостью, проходящей через точки
M,A,D
В1
D1
E
A1
С1
В
А
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – искомое сечение
М
D
С

22. Построить сечение параллелепипеда плоскостью, проходящей через точки М, К, Т

N
М
К
R
S
Х
Т

23. Выполните задания самостоятельно

м
т
к
м
Д
к
т
Постройте сечение: а) параллелепипеда;
б) тетраэдра
плоскостью, проходящей через точки М, Т, К.

24. Использованные ресурсы

Соболева Л. И. Построение сечений
Ткачева В. В. Построение сечений
тетраэдра и параллелепипеда
Гобозова Л. В. Задачи на построение
сечений
DVD-диск. Уроки геометрии Кирилла и
Мефодия. 10 класс, 2005
Обучающие и проверочные задания.
Геометрия. 10 класс (Тетрадь)/Алешина
Т.Н. – М.: Интеллект-Центр, 1998

Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.

С самого раннего детства мы сталкиваемся с сечениями. Режем хлеб, колбасу и другие продукты, обстругиваем палочку или карандаш ножом. Секущей плоскостью во всех этих случаях является плоскость ножа. Сечения (срезы кусочков) оказываются различными.

Сечение выпуклого многогранника есть выпуклый многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многоугольника, а стороны- линиями пересечения секущей плоскости с гранями.

Для построения прямой пересечения двух плоскостей достаточно найти две общие точки этих плоскостей и провести через них прямую. Это основано на следующих утверждениях:

1.если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости;

2.если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Как я уже сказал ппостроение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей. Вместе с тем, существуют определенные методы построения плоских сечений многогранников. Наиболее эффективными являются следующие три метода:

Метод следов

Метод внутреннего проектирования

Комбинированный метод.

В изучении геометрии и, в особенности, тех её разделов, где рассматриваются изображения геометрических фигур, изображения геометрических фигур помогают использования компьютерных презентаций. С помощью компьютера многие уроки геометрии становятся более наглядной и динамичной. Аксиомы, теоремы, доказательства, задачи на построения, задачи на построения сечений можно сопровождать последовательными построениями на экране монитора. Сделанные с помощью компьютера чертежи можно сохранять и вставлять их в другие документы.

Хочу показать несколько слайдов по теме: «Построения сечений в геометрических телах»

Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную прямую. Тогда искомая точка является точкой пересечения найденной прямой с данной. Проследим это на следующих слайдах.

Задача 1.

На ребрах тетраэдра DABC отмечены две точки М и N; М GAD, N б DC. Укажите точку пересечения прямой MN с плоскостью основания.

Решение: для того, чтобы найти точку пересечения прямой MN с плоскостью

основания мы продолжим АС и отрезок MN. Отметим точку пересечения этих прямых через X. Точка X принадлежит прямой MN и грани АС, а АС лежит в плоскости основания, значит точка X тоже лежит в плоскости основания. Следовательно, точка X есть точка пересечения прямой MN с плоскостью основания.

Рассмотрим вторую задачу. Немного усложним его.

Задача 2.

Дан тетраэдр DABC точки М и N, где М € DA, N С (DBC). Найти точку пересечения прямой MN с плоскостью ABC .

Решение: точка пересечения прямой MN с плоскостью ABC должна лежать в плоскости, которая содержит прямую MN и в плоскости основания. Продолжим отрезок DN до точки пересечения с ребром DC. Точку пересечения отметим через Е. Продолжим прямую АЕ и MN до точки их пересечения. Отметим X. Точка X принадлежит MN, значит она лежит на плоскости которая содержит прямую MN и X принадлежит АЕ, а АЕ лежит на плоскости ABC. Значит X тоже лежит в плоскости ABC. Следовательно X и есть точка пересечения прямой MN и плоскости ABC.

Усложним задачу. Рассмотрим сечение геометрических фигур плоскостями, проходящими через три данные точки.

Задача 3

На ребрах AC, AD и DB тетраэдра DABC отмечены точки М, N и Р. Построить сечение тетраэдра плоскостью MNP.

Решение: построим прямую, по которой плоскость MNP. Пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения ещё одной общей точки продолжим отрезок АВ и NP. Точку пересечения отметим через X, которая и будет второй общей точкой плоскости MNP и ABC. Значит эти плоскости пересекаются по прямой MX . MX пересекает ребро ВС в некоторой точке Е. Так как Е лежит на MX, а MX прямая принадлежащей плоскости MNP, значит РЕ принадлежит MNP. Четырёхугольник MNPE искомое сечение.

Задача 4

Построим сечение прямой призмы АВСА1В1С1 плоскостью проходящей через точки P, Q ,R, где R принадлежит (AA 1C 1C ), Р принадлежит В 1С1,

Q принадлежит АВ

Решение: Все три точки P,Q,R лежат в разных гранях, поэтому построить линию пересечения секущей плоскости с какой- либо гранью призмы мы пока не можем. Найдем точку пересечения PR с ABC. Найдем проекции точек Р и R на плоскость основания PP1 перпендикулярно ВС и RR1 перпендикулярна АС. Прямая P1R1 пересекается с прямой PR в точке X. X точка пересечения прямой PR с плоскостью ABC. Она лежит в искомой плоскости К ив плоскости основания, как и точка Q. XQ- прямая пересекающая К с плоскостью основания. XQ пересекает АС в точке К. Следовательно, KQ отрезок пересечения плоскости Х с гранью ABC. К и R лежат в плоскости Х и в плоскости грани АА1С1С. Проведем прямую KR и точку пересечения с A1Q отметим Е. КЕ является линией пересечения плоскости Х с этой гранью. Найдем линию пересечения плоскости Х с плоскостью граней BB1A1A. КЕ пересекается с А1А в точке У. Прямая QY есть линия пересечения секущей плоскости с плоскостью AA1B1B. FPEKQ- искомое сечение.

А вы знаете, что называется сечением многогранников плоскостью? Если вы пока сомневаетесь в правильности своего ответа на этот вопрос, то можете довольно просто себя проверить. Предлагаем пройти небольшой тест, представленный ниже.

Вопрос. Назовите номер рисунка, на котором изображено сечение параллелепипеда плоскостью?

Итак, правильный ответ – на рисунке 3.

Если вы ответите правильно, это подтверждает то, что вы понимаете, с чем имеете дело. Но, к сожалению, даже правильный ответ на вопрос-тест не гарантирует вам наивысших отметок на уроках по теме «Сечения многогранников». Ведь самым сложным является не распознавание сечений на готовых чертежах, хотя это тоже очень важно, а их построении.

Для начала сформулируем определение сечения многогранника. Итак, сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.

Теперь потренируемся быстро и безошибочно строить точки пересечения данной прямой с заданной плоскостью. Для этого решим следующую задачу.

Построить точки пересечения прямой MN с плоскостями нижнего и верхнего оснований треугольной призмы ABCA 1 B 1 C 1 , при условии, что точка M принадлежит боковому ребру CC 1 , а точка N – ребру BB 1 .

Начнем с того, что продлим на чертеже прямую MN в обе стороны (рис. 1). Затем, чтобы получить необходимые по уловию задачи точки пересечения, продлеваем и прямые, лежащие в верхнем и нижнем основаниях. И вот наступает самый сложный момент в решении задачи: какие именно прямые в обоих основаниях необходимо продлить, так как в каждом из них имеется по три прямые.

Чтобы правильно сделать заключительный шаг построения, необходимо определить, какие из прямых оснований находятся в той же плоскости, что и интересующая нас прямая MN. В нашем случае – это прямая CB в нижнем и C 1 B 1 в верхнем основаниях. И именно их и продлеваем до пересечения с прямой NM (рис. 2).

Полученные точки P и P 1 и есть точки пересечения прямой MN с плоскостями верхнего и нижнего оснований треугольной призмы ABCA 1 B 1 C 1 .

После разбора представленной задачи можно перейти непосредственно к построению сечений многогранников. Ключевым моментом здесь будут рассуждения, которые и помогут прийти к нужному результату. В итоге постараемся в итоге составить шаблон, который будет отражать последовательность действий при решении задач данного типа.

Итак, рассмотрим следующую задачу. Построить сечение треугольной призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки X, Y, Z, принадлежащие ребрам AA 1 , AC и BB 1 соответственно.

Решение: Выполним чертеж и определим, какие пары точек лежат в одной плоскости.

Пары точек X и Y, X и Z можно соединить, т.к. они лежат в одной плоскости.

Построим дополнительную точку, которая будет лежать в той же грани, что и точка Z. Для этого продлим прямые XY и СС 1 , т.к. они лежат в плоскости грани AA 1 C 1 C. Назовем полученную точку P.

Точки P и Z лежат в одной плоскости – в плоскости грани CC 1 B 1 B. Поэтому можем их соединить. Прямая PZ пересекает ребро CB в некоторой точке, назовем ее T. Точки Y и T лежат в нижней плоскости призмы, соединяем их. Таким образом, образовался четырехугольник YXZT, а это и есть искомое сечение.

Подведем итог. Чтобы построить сечение многогранника плоскостью, необходимо:

1) провести прямые через пары точек, лежащих в одной плоскости.

2) найти прямые, по которым пересекаются плоскости сечения и грани многогранника. Для этого нужно найти точки пересечения прямой, принадлежащей плоскости сечения, с прямой, лежащей в одной из граней.

Процесс построения сечений многогранников сложен тем, что в каждом конкретном случае он различен. И никакая теория не описывает его от начала и до конца. На самом деле есть только один верный способ научиться быстро и безошибочно строить сечения любых многогранников – это постоянная практика. Чем больше сечений вы построите, тем легче в дальнейшем вам будет это делать.

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Понравилась статья? Поделитесь ей

Распечатать статью